Practice Set

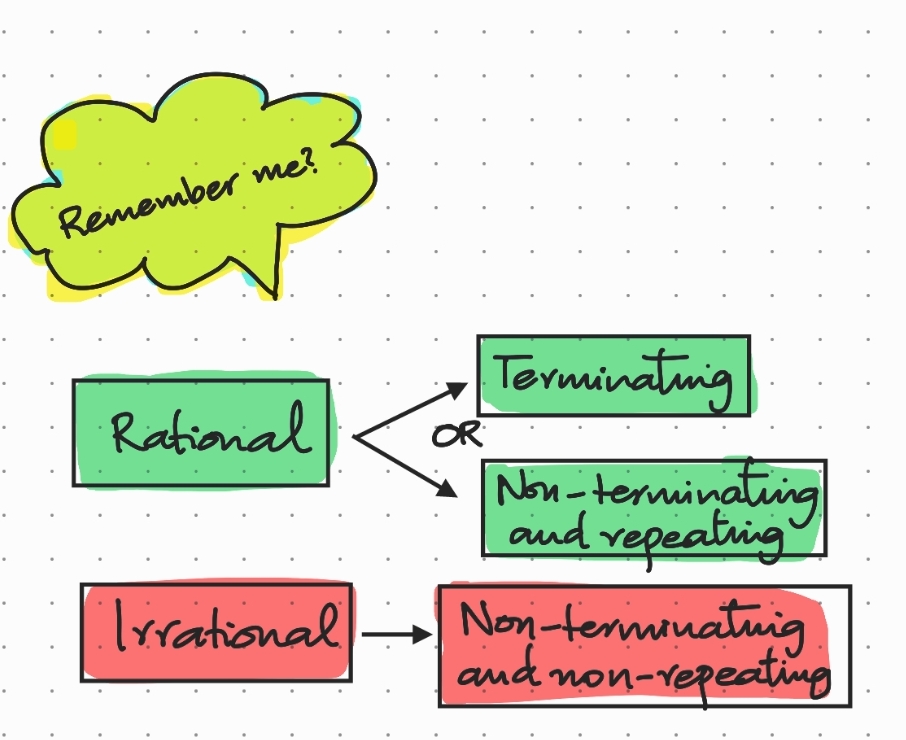
Let us first simplify the complicated-looking LHS using the LCM of the denominators, which is their product \((7-\sqrt5)(7+\sqrt5).\)

\(\frac{7+\sqrt5}{7-\sqrt5}-\frac{7-\sqrt5}{7+\sqrt5}=\frac{(7+\sqrt5)(7+\sqrt5)-(7-\sqrt5)(7-\sqrt5)}{(7-\sqrt5)(7+\sqrt5)}=\frac{(7+\sqrt5)^2-(7-\sqrt5)^2}{(7-\sqrt5)(7+\sqrt5)}\)

We use the identities \((a+b)^2=a^2+2ab+b^2 \) and \((a-b)^2=a^2-2ab+b^2\) in the numerator, and \((a+b)(a-b)=a^2-b^2\) in the denominator.

\(\therefore \frac{7+\sqrt5}{7-\sqrt5}-\frac{7-\sqrt5}{7+\sqrt5}=\frac{{\color{red}{(}}7^2+2(7)(\sqrt5)+(\sqrt5)^2 {\color{red}{)}}-{\color{blue}{(}}~7^2-2(7)(\sqrt5)+(\sqrt5)^2 {\color{blue}{)}}}{(7-\sqrt5)(7+\sqrt5)}=\frac{49+14\sqrt5+5-49+14\sqrt5-5}{49-5}=\frac{28\sqrt5}{44}=\frac{7\sqrt5 \times4}{44}=\frac{7\sqrt5}{11}\)

Thus, the initial equation can now be written as \(\frac{7\sqrt5}{11}=p-7\sqrt5q.\)

\(\therefore \frac{7\sqrt5}{11}={\color{red}{0}}-7\sqrt5\times {\color{blue}{-\frac{1}{11}}}={\color{red}{p}}-7\sqrt5{\color{blue}{q}}\)

Comparing both sides of the above equation, we get \(p=0\) and \(q=-\frac{1}{11}.\)

We have \(x=\frac{3-\sqrt{13}}{2}.—(1)\)

\(\implies x^2=(\frac{3-\sqrt{13}}{2})^2=\frac{(3-\sqrt{13})^2}{2^2}=\frac{3^2-2(3)(\sqrt{13})+(\sqrt{13})^2}{4}=\frac{9-6\sqrt{13}+13}{4}=\frac{22-6\sqrt{13}}{4}=\frac{11-3\sqrt{13}}{2}\)

(\(\because (a-b)^2=a^2-2ab+b^2\))

\(\therefore \frac{1}{x^2}=\frac{1}{(\frac{11-3\sqrt{13}}{2})}=\frac{2}{11-3\sqrt{13}}\)

Combining \((1)\) and \((2),\) we have:

\( x^2+\frac{1}{x^2}=\frac{11-3\sqrt{13}}{2}+\frac{2}{11-3\sqrt{13}}=\frac{(11-3\sqrt{13})(11-3\sqrt{13})+2(2)}{2(11-3\sqrt{13})}=\frac{(11-3\sqrt{13})^2+4}{2(11-3\sqrt{13})}=\frac{11^2-2(11)(3\sqrt{13})+(3\sqrt{13})^2+4}{2(11-3\sqrt{13})}\)

\(\therefore x^2+\frac{1}{x^2}=\frac{121-66\sqrt{13}+117+4}{2(11-3\sqrt{13})}=\frac{242-66\sqrt{13}}{2(11-3\sqrt{13})}=\frac{22(11-3\sqrt{13})}{2(11-3\sqrt{13})}=\frac{22}{2}=11\)

Thus, we have \(x^2+\frac{1}{x^2}=11.\)

1. A number whose decimal expansion is either terminating or is non-terminating and repeating is a rational number.
2. A number whose decimal expansion is non-terminating and non-repeating is irrational.

(i) \(0.2222\)

The given decimal is terminating. Hence, it represents a rational number.

(ii) \(0.2222…\)

The given decimal is non-terminating and repeating. Thus, \(0.2222…=0.\overline{2}\) represents a rational number.

(iii) \(0.22228649123…\)

The given decimal is non-terminating and non-repeating, and hence represents an irrational number.

(iv) \(1.5042056719362740\)

The given decimal is terminating, and hence represents a rational number.

Let us consider \(\sqrt{10+\sqrt{24}+\sqrt{60}+\sqrt{40}}.\) Replacing \(\color{red}{10}\) by \({\color{red}{2+3+5}},\) we get:

\(\sqrt{{\color{red}{10}}+\sqrt{24}+\sqrt{60}+\sqrt{40}}=\sqrt{{\color{red}{2+3+5}}+\sqrt{24}+\sqrt{60}+\sqrt{40}}=\sqrt{2+3+5+2\sqrt6+2\sqrt{15}+2\sqrt{10}}\)

\(=\sqrt{(\sqrt2)^2+(\sqrt3)^2+(\sqrt5)^2+2\sqrt2\sqrt3+2\sqrt3\sqrt5+2\sqrt2\sqrt5}\)

\(=\sqrt{({\color{red}{\sqrt{2}}}+{\color{blue}{\sqrt{3}}}+{\color{pink}{\sqrt{5}}})^2}~ ~ ~ ~ ~ (\because {\color{red}{a}}^2+{\color{blue}{b}}^2+{\color{pink}{c}}^2+2{\color{red}{a}}{\color{blue}{b}}+2{\color{blue}{b}}{\color{pink}{c}}+2{\color{red}{a}}{\color{pink}{c}}=({\color{red}{a}}+{\color{blue}{b}}+{\color{pink}{c}})^2)\)

\(=\sqrt2+\sqrt3+\sqrt5\)

\(\therefore \sqrt{10+\sqrt{24}+\sqrt{60}+\sqrt{40}}=\sqrt2+\sqrt3+\sqrt5~ ~ —(1)\)

But, we are given that \(\sqrt{10+\sqrt{24}+\sqrt{60}+\sqrt{40}}=\sqrt{a}+\sqrt{b}+\sqrt{c},\) where \(a<b<c.\)

Thus, comparing with \((1),\) we get:

\(a=2, b=3, c=5 ~ ~ ~ (\because a<b<c)\)

\(\therefore a+b-c=2+3-5=5-5=0\)

We are given that \(x=9+4\sqrt5.\)

\(\implies \sqrt{x}=\sqrt{\underline{9}+4\sqrt5}=\sqrt{\underline{5+4}+4\sqrt5}=\sqrt{({\color{red}{\sqrt5}})^2+({\color{blue}{2}})^2+2({\color{red}{\sqrt5}})({\color{blue}{2}})}\)

\(= \sqrt{({\color{red}{\sqrt5}}+{\color{blue}{2}})^2}~ ~ (\because {\color{red}{a}}^2+{\color{blue}{b}}^2+2{\color{red}{a}}{\color{blue}{b}}=({\color{red}{a}}+{\color{blue}{b}})^2)\)

\(\therefore \sqrt{x}=\sqrt5+2~ ~ ~ ~ —(1)\)

\(\implies \frac{1}{\sqrt{x}}=\frac{1}{\sqrt5+2}=\frac{1}{\sqrt5+2} \times \frac{\color{red}{\sqrt5-2}}{\color{red}{\sqrt5-2}}=\frac{\sqrt5-2}{(\sqrt5+2)(\sqrt5-2)}=\frac{\sqrt5-2}{(\sqrt5)^2-(2)^2}~ ~ ~ (\because (a+b)(a-b)=a^2-b^2)\)

\(\therefore \frac{1}{\sqrt{x}}=\frac{\sqrt5-2}{5-4}=\frac{\sqrt5-2}{1}=\sqrt5-2~ ~ ~ ~ —(2)\)

\(\therefore (1)\text{ and }(2)\implies \sqrt{x}+\frac{1}{\sqrt{x}}=\sqrt5+2+\sqrt5-2=2\sqrt5\)