Chapter 1 – Number Systems

Let us understand the concepts of the chapter in detail, shall we?

Before understanding what rational numbers are, let us quickly recall what natural numbers, whole numbers and integers are. It is good practice to refresh our memory on what we already know before we go on to learn something new! Because if the foundation isn’t strong, there is really no point in building skyscrapers out of it! Watch the following video to quickly recapitulate the different kinds of numbers we already know and then we will meet our new friend, Mr. Rational Number!

Alright! So that was Mr. Rational Number. He seems nice, does he not? But, how is he related to Mr. Natural Number, Mr. Whole Number and Mr. Integer whom we already know? How different are they? Watch the following video to find out.

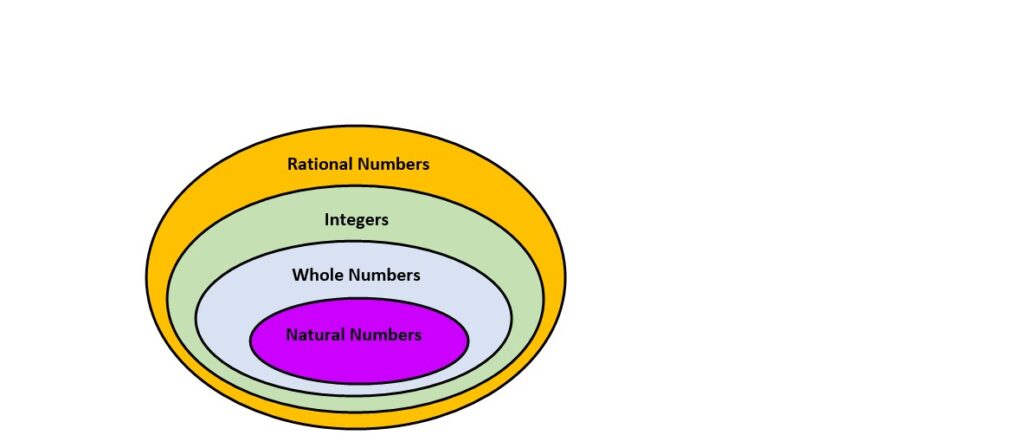
Well, well, well. That’s how they are related. One nice family, don’t you think?

Okay. Now, do you remember how I mentioned in the first video that a rational number is like a fraction? Well, how like and how much alike? Also, what are equivalent rational numbers? Watch the video to find out the new (but not-so-new!) definition of Mr. Rational Number.

Cool. Let us move forward, my friend. Let us look at how there are so, so many rational numbers between any two numbers.

But, before that take a break and refresh your brain!

Welcome back, mi amigo.

Oho! That is how you find rational numbers between any two integers (and also between any two rational numbers!). I hope both the methods are clear, my friend. I know you will only pick the second method because it is easy-peasy. But, please try to understand how beautiful the first method is too.

Okay. So, that was about rational numbers.

Natural Numbers -> Whole Numbers -> Integers -> Rational Numbers

Phew! This must mean we have all the numbers on the number line finally. Right?

Well………….!

No. There are a few more numbers!

But, how? Where? And most importantly, why??????? (😭😭😭😭)

Haha! Hold on, mi amigo. These new numbers are called irrational numbers. Watch the video below to know all about them.

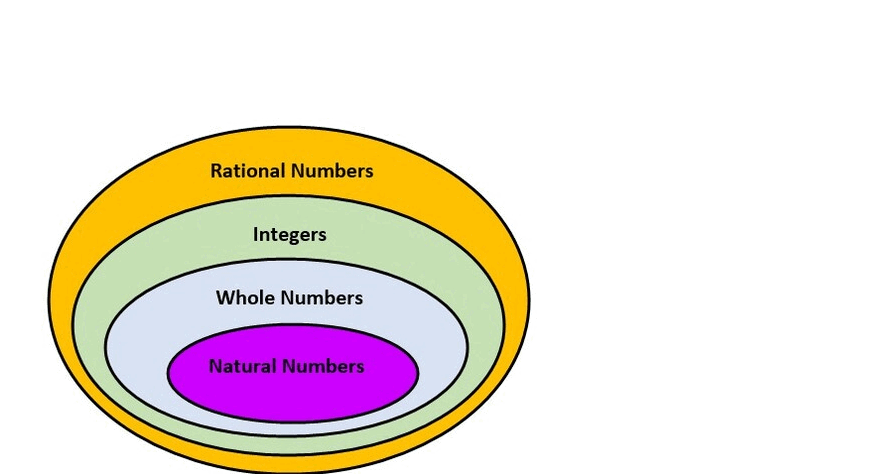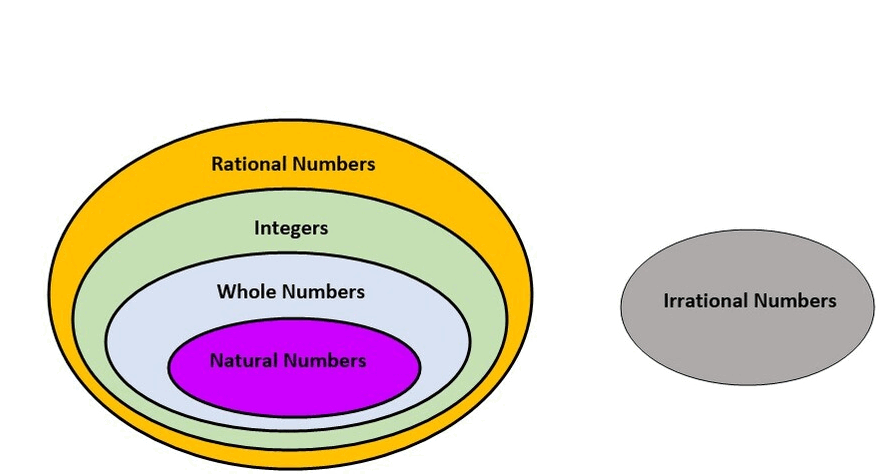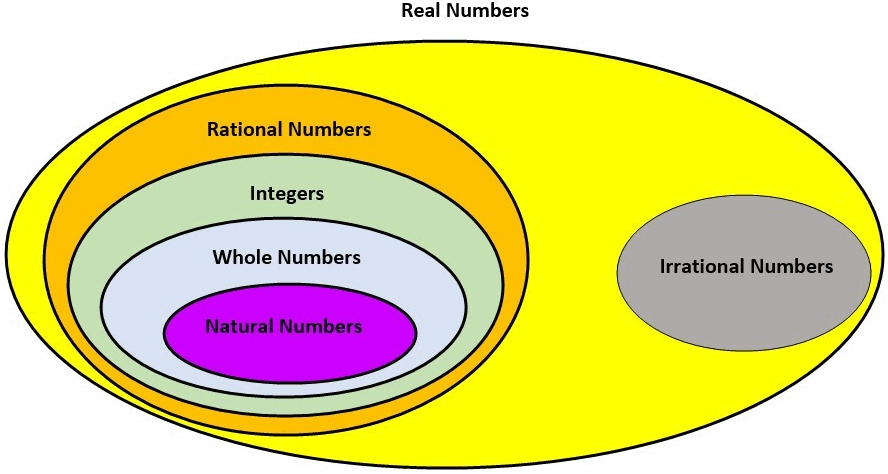
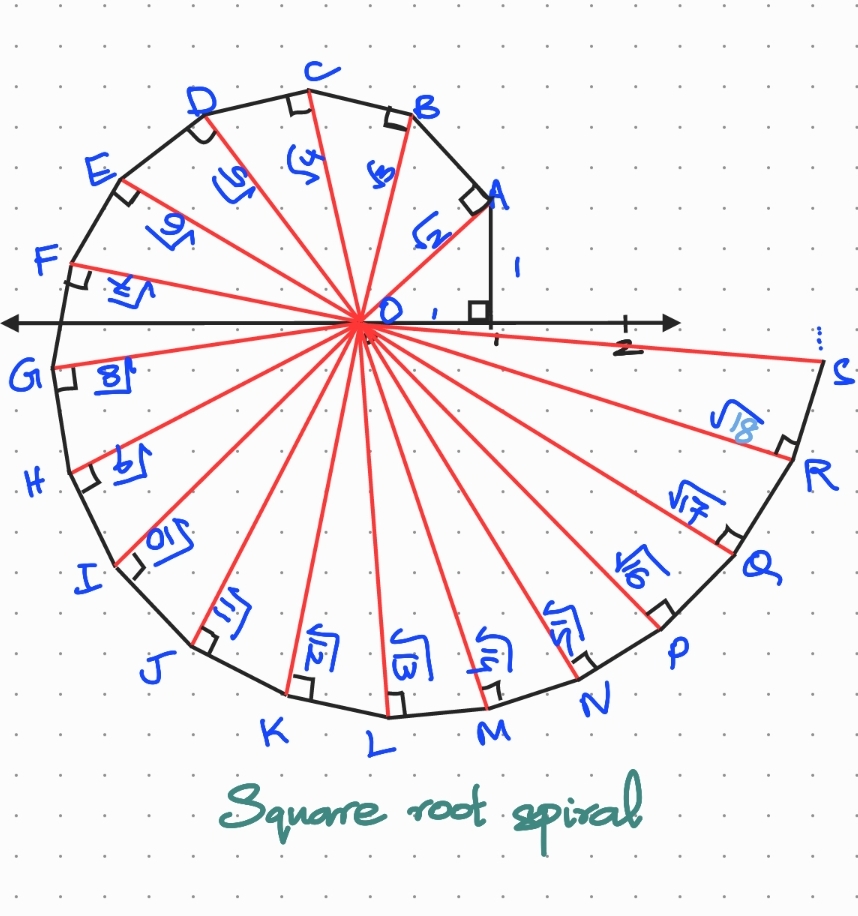
Also, here is the square root spiral diagram that I promised you! It does look beautiful, does it not? 🙂

Now, we have seen what a rational number is and what an irrational number is. But, this definition of an irrational number that it is not rational is not always enough. We need better ways to identify irrational numbers. This is where the concept of decimal expansion serves helpful. We can just look at the decimal expansion of a real number and deduce if it corresponds to a rational or an irrational number. Impressive, right? Well, what are you waiting for? Get your Sherlock Holmes on and dive in to the video to learn more.

So, given a terminating decimal or a repeating decimal, we can immediately say that it corresponds to a rational number. But, any rational number can be written in the form \(\frac{p}{q},\) where \(p\) and \(q\) are integers and \(q\neq0,\) right? So, how would you express a terminating or a repeating decimal in this \(\frac{p}{q}\) form then? Watch the video to find out, my friend.

Up next, we represent real numbers on the very real number line (see what I did there? :P). We start with the easy-peasy example of a terminating decimal and then move onto a repeating decimal. Go get your premium Sherlock kit that has the magnifier and let’s get to it, my friend.

(The remaining videos of the chapter will be uploaded soon. I thank you for your grace and patience, my friend. )