1. Number Systems

1. Is zero a rational number? Can you write it in the form \(\frac{p}{q},\) where \(p\) and \(q\) are integers and \(q\neq 0\)?

Solution:

A number that can be written in the form \(\frac{{\color{red}{p}}}{{\color{green}{q}}}\) where \(p\) and \(q\) are integers and \(q\neq 0\) is called a rational number.

Note that \(0=\frac{{\color{red}{0}}}{{\color{green}{1}}},\) where \(0\) and \(1\) are integers and \(1\neq 0.\)

Thus, zero is a rational number.

2. Find six rational numbers between \(3\) and \(4.\)

Solution:

Note the following:

1. There are infinitely many rational numbers between any two numbers.
2. \(\frac{{\color{red}{r}}+{\color{blue}{s}}}{2}\) is a rational number that lies between the integers \(\color{red}{r}\) and \({\color{blue}{s}}.\)

Method 1 (When you have all the time in the world!):

Let us consider the integers \(3\) and \(4.\)

\(\frac{{\color{red}{3}}+{\color{blue}{4}}}{2}=\frac{7}{2}\) is a rational number between \(\color{red}{3}\) and \({\color{blue}{4}}.\)

\(\frac{{\color{red}{3}}+{\color{blue}{\frac{7}{2}}}}{2}=\frac{\frac{6+7}{2}}{2}=\frac{13}{4}\) is a rational number between \(\color{red}{3}\) and \({\color{blue}{\frac72}},\) and hence between \(3\) and \(4.\)

\(\frac{{\color{red}{\frac{7}{2}}}+{\color{blue}{4}}}{2}=\frac{\frac{15}{2}}{2}=\frac{15}{4}\) is a rational number between \({\color{red}{\frac72}}\) and \({\color{blue}{4}},\) and hence between \(3\) and \(4.\)

\(\frac{{\color{red}{3}}+{\color{blue}{\frac{13}{4}}}}{2}=\frac{\frac{25}{4}}{2}=\frac{25}{8}\) is a rational number between \(\color{red}{3}\) and \({\color{blue}{\frac{13}{4}}},\) and hence between \(3\) and \(4.\)

\(\frac{{\color{red}{\frac{15}{4}}}+{\color{blue}{4}}}{2}=\frac{\frac{31}{4}}{2}=\frac{31}{8}\) is a rational number between \(\color{red}{\frac{15}{4}}\) and \({\color{blue}{4}},\) and hence between \(3\) and \(4.\)

\(\frac{{\color{red}{3}}+{\color{blue}{\frac{25}{8}}}}{2}=\frac{\frac{49}{8}}{2}=\frac{49}{16}\) is a rational number between \(\color{red}{3}\) and \({\color{blue}{\frac{25}{8}}},\) and hence between \(3\) and \(4.\)

Thus, \(\frac72,\frac{13}{4},\frac{15}{4},\frac{25}{8},\frac{33}{8}\) and \(\frac{49}{16}\) are six rational numbers between \(3\) and \(4.\)

(Don’t trust me? Check them on the number line given below!)

(This method can however prove time-consuming if we need to find many rational numbers between two integers!)

Method 2 (Easy-peasy):

We use the concept of equivalent rational numbers to find rational numbers between \(3\) and \(4.\)

\(3=\frac{21}{7}, ~ 4=\frac{28}{7}\)

(Why did I write \(3\) as a fraction with \(7\) in the denominator, you ask? Because we need six rational numbers between \(3\) and \(4.\) Had we needed five rational numbers, we would have written \(3\) as \(\frac{18}{6}\) and \(4\) as \(\frac{24}{6}.\) )

We know that \(\frac{22}{7},\frac{23}{7},\frac{24}{7},\frac{25}{7},\frac{26}{7}\) and \(\frac{27}{7}\) lie between \(\frac{21}{7}\) and \(\frac{28}{7},\) and hence between \(3\) and \(4.\)

Also, these numbers are rational since they are expressed in the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q\neq 0.\)

Thus, \(\frac{22}{7},\frac{23}{7},\frac{24}{7},\frac{25}{7},\frac{26}{7}\) and \(\frac{27}{7}\) are six rational numbers between \(3\) and \(4.\)

3. Find five rational numbers between \(\frac{3}{5}\) and \(\frac{4}{5}.\)

Solution:

(We could use either of the methods mentioned above.)

Using the concept of equivalent rational numbers, we have:

\(\frac{3}{5}= \frac{3\times {\color{orange}{6}}}{5\times {\color{orange}{6}}}=\frac{18}{30} \)

\(\frac45=\frac{4\times {\color{orange}{6}}}{5\times {\color{orange}{6}}}=\frac{24}{30}\)

(Again, we are multiplying by \(6\) because we need \(5\) rational numbers between \(\frac35\) and \(\frac45.\))

We know that \(\frac{19}{30},\frac{20}{30},\frac{21}{30},\frac{22}{30}\) and \(\frac{23}{30}\) lie between \(\frac{18}{30}\) and \(\frac{24}{30},\) that is in between \(\frac35\) and \(\frac45.\) Also, these are rational numbers as they are in the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q\neq 0.\)

Thus, these are 5 rational numbers between \(\frac35\) and \(\frac45.\)

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

(ii) Every integer is a whole number.

(iii) Every rational number is a whole number.

Solution:

(i) Natural numbers \(\to {\color{orange}{1}},{\color{orange}{2}},{\color{orange}{3}},{\color{orange}{4}},{\color{orange}{5}},\color{orange}{…}\)

Whole numbers \(\to {\color{blue}{0}},{\color{orange}{1}},{\color{orange}{2}},{\color{orange}{3}},{\color{orange}{4}},{\color{orange}{5}},\color{orange}{…}\)

Every number on the first list is on the second list. Thus, every natural number is a whole number. In fact, the collection of whole numbers is formed by adding zero to the collection of natural numbers.

(Extra fact: Not every whole number is a natural number. In fact, \(0\) is a whole number, but not a natural number.)

(ii) Integers \({\color{blue}{…}},{\color{blue}{-3}},{\color{blue}{-2}},{\color{blue}{-1}},{\color{orange}{0}},{\color{orange}{1}},{\color{orange}{2}},{\color{orange}{3}},\color{orange}{…}\)

Whole numbers \(\to {\color{orange}{0}},{\color{orange}{1}},{\color{orange}{2}},{\color{orange}{3}},\color{orange}{…}\)

Not every number on the first list is on the second list. In fact, negative integers (\({\color{blue}{-1}},{\color{blue}{-2}},{\color{blue}{-3}}…\)) are not on the list. Thus, every integer need not be a whole number.

(Extra fact: Every whole number is an integer. )

(iii) \(\frac35\) is a rational number as it is in the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q\neq 0.\) But, \(\frac35\) is not a whole number. There are several other similar examples. Thus, every rational number need not be a whole number.

(Extra fact: Every whole number is a rational number. A whole number \(a\) can be written as \(\frac{a}{1}\)) where \(a\) and \(1\) are integers and \(1\neq 0.\) Note that since \(a\) is a whole number, it is also an integer.

1. State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number.

(ii) Every point on the number line is of the form \(\sqrt{m},\) where \(m\) is a natural number.

(iii) Every real number is an irrational number.

Solution:

(i) The collection of all real numbers is made by the collection of all rational numbers and the collection of all irrational numbers put together.

Thus, every irrational number is a real number.

(ii) Consider the point zero on the number line. There exists no natural number \(m\) such that \(0=\sqrt{m}.\)

(This is because \(\sqrt{m}=0\implies m=0,\) which is not a natural number. )

Similarly, we cannot express negative integers as square roots of natural numbers.

Thus, the given statement that every point on the number line is of the form \(\sqrt{m}\) where \(m\) is a natural number is not true.

(iii) Every real number is either rational or irrational. Thus, the statement that every real number is irrational is not true.

2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Solution:

Consider the positive integer \(9.\)

\(\sqrt{9}=\sqrt{3\times 3}=3=\frac31,\) a rational number as \(3\) and \(1\) are integers and \(1\neq 0.\)

Thus, we have a positive integer the square root of which is a rational number.

There are several other examples like \(\sqrt4=2=\frac21,\sqrt{16}=4=\frac41,\sqrt{25}=5=\frac51\) and so on.

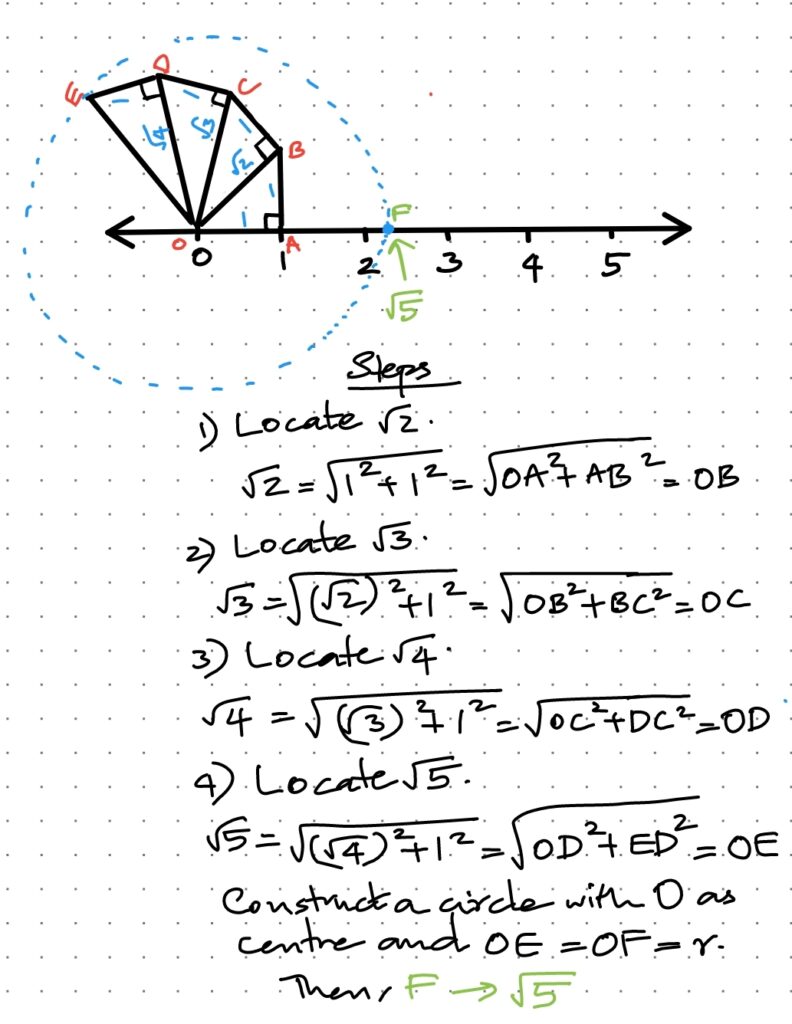
3. Show how \(\sqrt5\) can be represented on the number line.

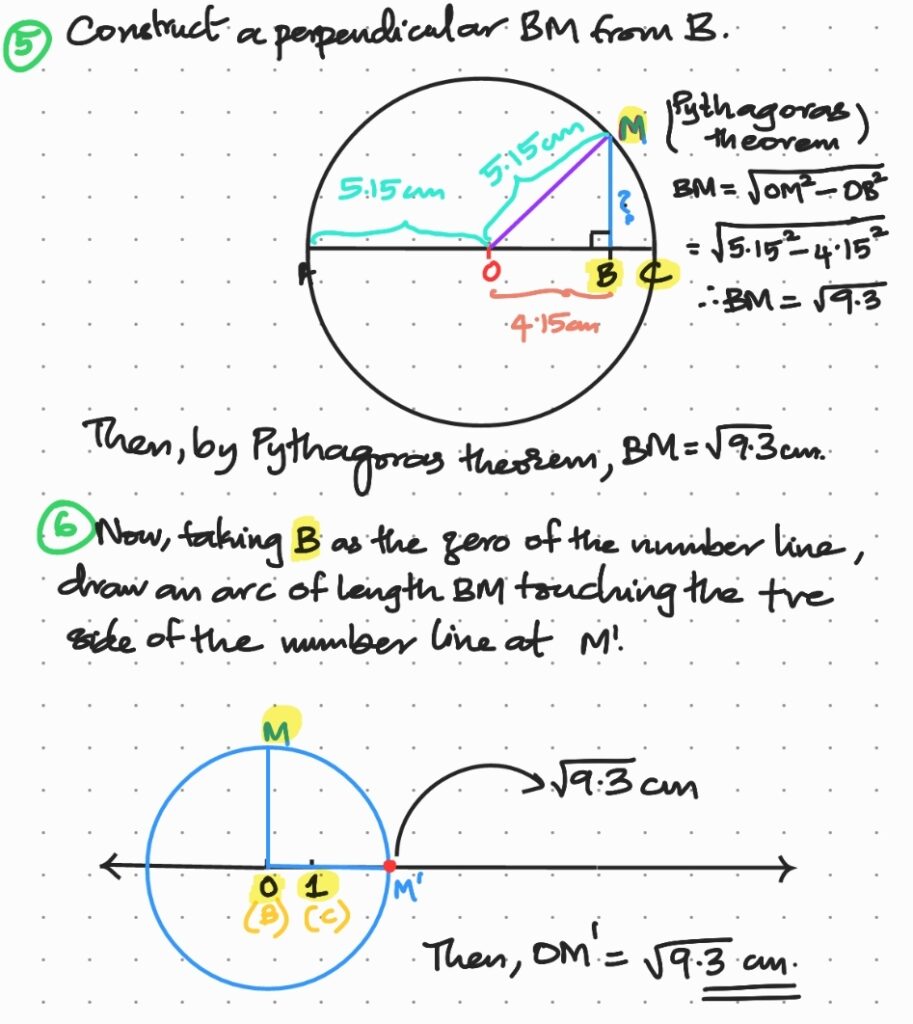
To locate \(\sqrt5\) on the number line, we draw the perpendicular \(AB\) of \(1\) unit to the number line at \(B.\) Then, applying Pythagoras theorem to the right-angled triangle, we have:

\(OB^2=OA^2+AB^2=1^2+1^2=2\implies OB=\sqrt2\) units

Taking \(OB\) as the base and dropping a perpendicular \(BC\) of \(1\) unit at \(B\) and forming the right-angled triangle \(\triangle OBC,\) we have:

\(OC^2=OB^2+BC^2=(\sqrt2)^2+1^2=2+1=3\implies OC=\sqrt3\)

Continuing this process, we have:

\(OD^2=OC^2+CD^2=(\sqrt3)^2+1^2=4\implies OC=\sqrt4=2\) units

\(OE^2=OD^2+ED^2=2^2+1^2=5\implies OE=\sqrt5\) units

Now, taking \(O\) as the centre and \(OE=\sqrt5\) units as the radius, draw an arc that touches the positive side of the number line at \(F.\)

Then, this point corresponds to \(\sqrt5\) on the number line.

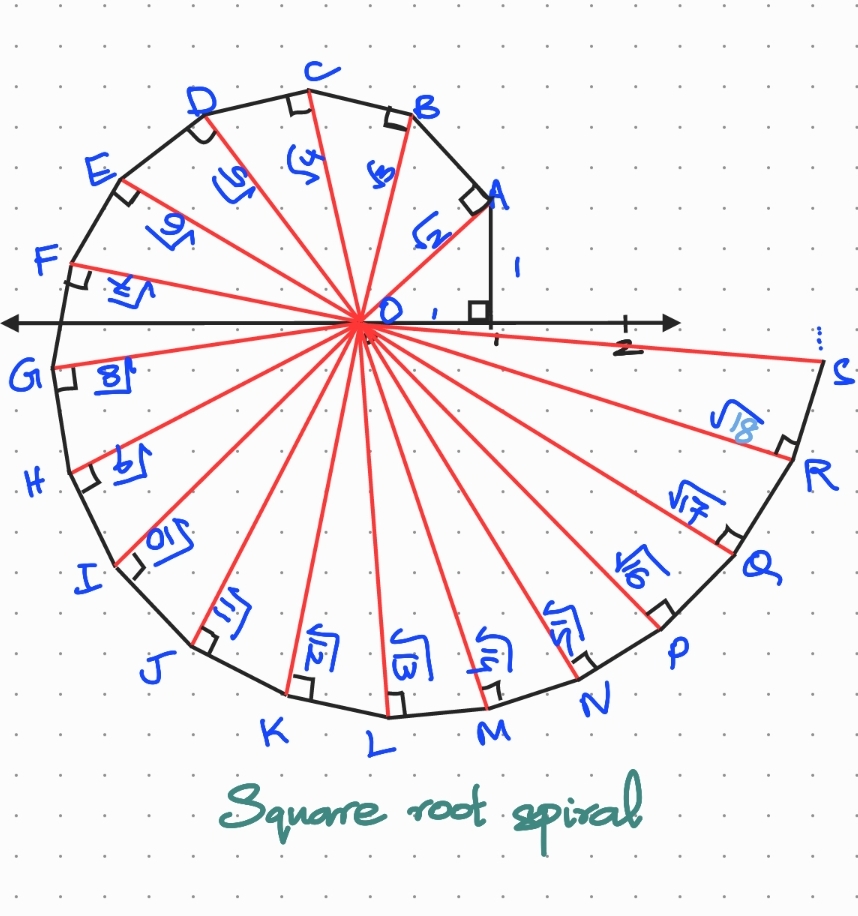
4. Construct the square root spiral.

(We use the steps mentioned above to locate \(\sqrt5\) on the number line and repeat the procedure!)

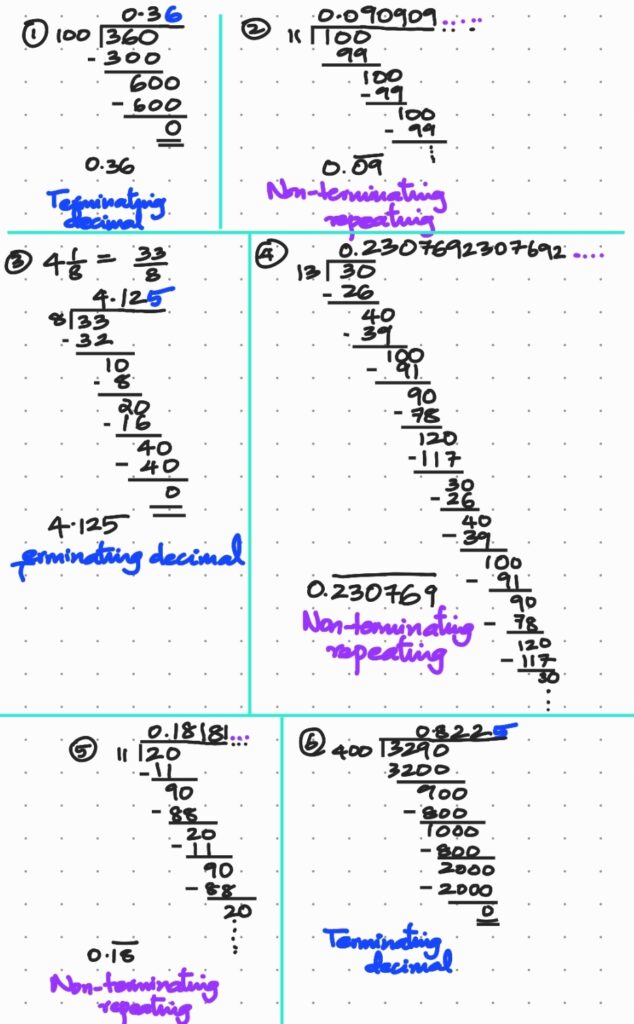
1. Write the following in decimal form and say what kind of decimal expansion each has :

(i) \(\frac{36}{100}\) (ii) \(\frac{1}{11}\) (iii) \(4\frac{1}{8}\) (iv) \(\frac{3}{13}\) (v) \(\frac{2}{11}\) (vi) \(\frac{329}{400}\)

Solution:

2. You know that \(\frac17=0.\overline{142857}\). Can you predict what the decimal expansions of \(\frac27,\frac37,\frac47,\frac57,\frac67\) are, without actually doing the long division? If so, how?

Solution:

When \(\color{red}{1}\) is divided by \({\color{red}{7}},\) we get \(\color{red}{0.\overline{142857}}\) as the quotient and \(\color{red}{1}\) as the remainder as shown below.

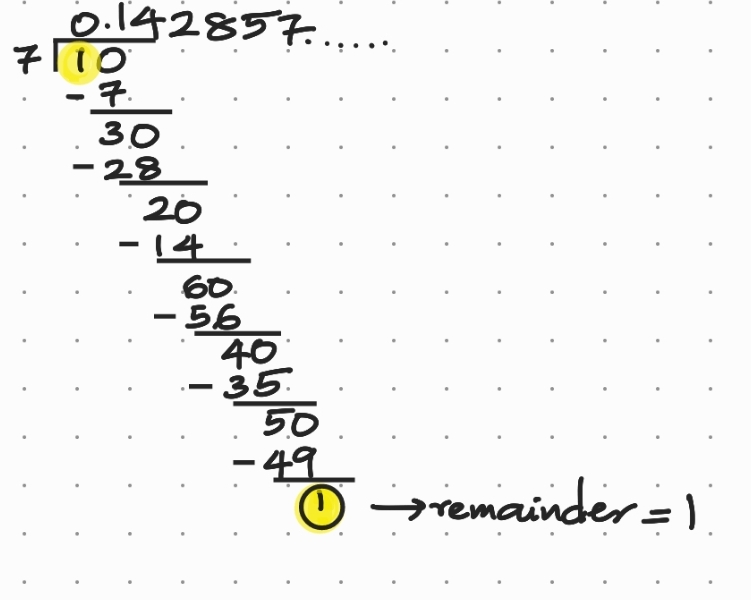
\(\therefore \) The decimal expansion of \(\frac17\) is \(0.\overline{142857}.\)

Note that \(\frac{{\color{blue}{2}}}{{\color{red}{7}}}=\color{blue}{2}\times {\color{red}{\frac17}}.\) Thus, the quotient and the remainder when \(\color{blue}{2}\) is divided by \(\color{red}{7}\) are \(\color{blue}{2}\times \color{red}{0.\overline{142857}}=\color{blue}{0.\overline{285714}}\) and \(\color{blue}{2} \times \color{red}{1}=2.\)

Thus, the decimal expansion of \(\frac27\) is \(0.\overline{285714}.\)

We may verify the same by performing the long division.

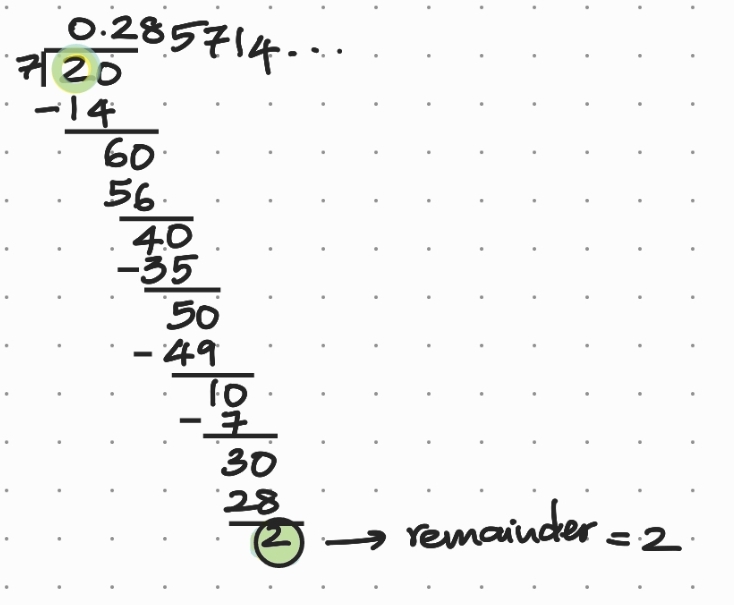
Similarly, the decimal expansions of the following are:

\(\frac37=3\times \frac17=3\times 0.\overline{142857}=0.\overline{428571}\)

\(\frac47=4\times \frac17=4\times 0.\overline{142857}=0.\overline{571428}\)

\(\frac57=5\times \frac17=5\times 0.\overline{142857}=0.\overline{714285}\)

\(\frac67=6\times \frac17=6\times 0.\overline{142857}=0.\overline{857142}\)

3. Express the following in the form \(\frac{p}{q},\) where \(p\) and \(q\) are integers and \(q\neq 0.\)

(i) \(0.\overline{6}\) (ii) \(0.4\overline{7}\) (iii) \(0.\overline{001}\)

Solution:

(i) Let \(y=0.\overline{6}.~ ~ ~ —(1)\)

Then, multiplying both sides by \(10,\) we get:

\(10\times y=10\times 0.\overline{6}\implies 10y=6.\overline{6}~ ~ ~ —(2)\)

\((2)-(1)\implies 10y-y=6.\overline{6}-0.\overline{6}\implies 9y=6\implies y=\frac69=\frac23\)

Thus, expressing \(0.\overline{6}\) as a rational number, we get \(\frac23.\)

(ii) Let \(y=0.4\overline{7}.~ ~ ~ —(1)\)

Then, multiplying both sides by \(10,\) we get:

\(10\times y=10\times 0.4\overline{7}\implies 10y=4.\overline{7}~ ~ ~ —(2)\)

Multiplying \((2)\) by \(10,\) we get:

\(10\times 10y=10\times 4.\overline{7}\implies 100y=47.\overline{7}~ ~ ~ —(3)\)

\((3)-(2)\implies 100y-10y=47.\overline{7}-4.\overline{7}\implies 90y=43\implies y=\frac{43}{90}\)

Thus, expressing \(0.4\overline{7}\) as a rational number, we get \(\frac{43}{90}.\)

(iii) Let \(y=0.\overline{001}.~ ~ ~ —(1)\)

Multiplying \((1)\) by \(1000,\) we get:

\(1000y=1000\times 0.\overline{001}=001.\overline{001}=1.\overline{001} ~ ~ ~ —(2)\)

\((2)-(1)\implies 1000y-y=1.\overline{001}-0.\overline{001}\implies 999y=1\implies y=\frac{1}{999}\)

Thus, expressing \(0.\overline{001}\) as a rational number, we get \(\frac{1}{999}.\)

4. Express \(0.9999…\) in the form \(\frac{p}{q}.\) Are you surprised by your answer? Discuss with your teachers and classmates why the answer makes sense.

Solution:

Let \(y=0.9999…=0.\overline{9}. ~ ~ ~ —(1)\)

Multiplying both sides of \((1)\) by \(10,\) we get:

\(10y=10\times 0.\overline{9}=9.\overline{9}~ ~ ~ —(2)\)

\((2)-(1)\implies 10y-y=9.\overline{9}-0.\overline{9}=9\implies 9y=9\implies y=1\)

Thus, expressing the repeating decimal \(0.\overline{9}\) as a rational number, we get \(1.\) This is because \(0.999999….\) is very close to 1 and the difference between the two negligible.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.

Solution:

The maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) is \(16.\) Why, you ask?

Let me explain this to you with a smaller number than \(17\) so that it is a little easier to understand. Let us consider the fraction, say \(\frac17.\)

\(\frac17=0.\overline{142857}~ ~ ~ –(1)\)

Multiplying both sides by \(10^6,\) we get:

\(10^6\times \frac17=10^6\times 0.\overline{142857}1\implies \frac{10^6}{7}=142857.\overline{142857}~ ~ ~ —(2)\)

\((2)-(1)\implies \frac{10^6}{7}-\frac17=142857.\overline{142857}-0.\overline{142857}=142857\)

\(\implies \frac17 \times (10^6-1)=142857\implies \frac{1}{\color{blue}{7}}=\frac{142857}{10^{\color{blue}{6}}-1}~ ~ ~ —(3)\)

Note that \(\color{blue}{6}\) is the period of \(\frac{1}{7}\) as there are \(\color{blue}{6}\) digits in the repeating block of the decimal expansion of \(\frac17.\)

(What is a period, you ask? The number of digits that repeat in a decimal is called its period. \(1,4,2,8,5\) and \(7\) are six digits in total. Thus, the period of \(\frac17\) is \(6.\))

This is true for any \(\frac{1}{n}.\) The maximum period or the maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{n}\) (where \(n\) is a natural number) is \(n-1.\)

Thus, the maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) is \(16.\)

In fact, performing the long division, we get:

\(\frac{1}{17}=0.\overline{0588235294117647}\)

Thus, the period of \(\frac{1}{17}\) is indeed \(16.\)

6. Look at several examples of rational numbers in the form \(\frac{p}{q}~ ~ (q\neq 0),\) where \(p\) and \(q\) are integers with no common factors other than \(1\) and having terminating decimal representations (expansions). Can you guess what property \(q\) must satisfy?

Solution:

Let us consider the following rational numbers in the form \(\frac{p}{q}\) where \(p\) and \(q\) are co-prime integers (just a fancy name for saying they have no common factors other than \(1\)) and have terminating decimal expansions.

\(\frac12=0.5~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{1}{5}=0.2~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{3}{40}=0.075\)

\(\frac14=0.25~ ~ ~ ~\) \(~ ~ ~ ~ \frac{1}{10}=0.1~ ~ ~ ~ \) \(~ ~ ~ ~\frac{1}{25}=0.04\)

Now, let us look at their denominators in particular.

\(\frac{1}{2}=\frac{1}{2^1}~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{1}{5}=\frac{1}{5^1}~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{3}{40}=\frac{3}{2^3\times 5^1}\)

\(\frac14=\frac{1}{2^2}~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{1}{10}=\frac{1}{2^1\times 5^1}~ ~ ~ ~ \) \(~ ~ ~ ~ \frac{1}{25}=\frac{1}{5^2}\)

Thus, we see that the denominators of these rational numbers are of the form \(2^a\times 5^b,\) where \(a\) and \(b\) are whole numbers.

Thus, if the denominator is either a multiple of \(2\) or a multiple of \(5\) or a multiple of \(2\times 5=10,\) then the decimal expansion of the rational number is terminating no matter what the numerator is.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution:

We know that any irrational number has its decimal expansion to be non-terminating and non-repeating.

We also know that \(\sqrt2,\sqrt3\) and \(\sqrt5\) are irrational numbers.

\(\sqrt2=1.4142135623731….\)

\(\sqrt3=1.7320508075689….\)

\(\sqrt5=2.2360679774998….\)

Thus, these are three examples of numbers whose decimal expansion is non-terminating and non-repeating.

8. Find three different irrational numbers between the rational numbers \(\frac57\) and \(\frac{9}{11}.\)

Solution:

\(\frac57=0.\overline{714285}, \frac{9}{11}=0.\overline{81}\)

Since any number whose decimal expansion is non-terminating and non-recurring is an irrational number, the following numbers are irrational:

\(0.72956186…, 0.801864362193285…, 0.80497492817…\)

Also, these numbers lie between \(\frac57\) and \(\frac{9}{11}.\)

Thus, \(0.72956186…, 0.801864362193285…\) and \(0.80497492817…\) are three irrational numbers between \(\frac57\) and \(\frac{9}{11}.\)

9. Classify the following numbers as rational or irrational:

(i) \(\sqrt{23}\) (ii) \(\sqrt{225}\) (iii) \(0.3796\) (iv) \(7.478478…\) (v) \(1.101001000100001…\)

Solution:

(i) \(\sqrt{23}=4.795831523…\) is a non-terminating non-repeating decimal. Hence, \(\sqrt{23}\) is an irrational number.

(Extra fact! – If \(n\) is not a perfect square, then \(\sqrt{n}\) is irrational.

What is a perfect square, you ask? A number that can be expressed as a square of an integer is called a perfect square. \(25\) is a perfect square as \(25=5^2.\)

\(23\) is not a perfect square as \(23\) cannot be expressed as the square of an integer.

So, since \(23\) is not a perfect square, we must have \(\sqrt{23}\) to be irrational.)

(ii) \(\sqrt{225}=\sqrt{15\times 15}=15\) is a rational number as \(15=15.0\) is a terminating decimal!

(iii) \(0.3796\) is a terminating decimal and hence a rational number.

(iv) \(7.478478…=7.\overline{478}\) is a non-terminating and repeating decimal and hence is a rational number.

(v) \(1.101001000100001…\) is a non-terminating and non-recurring decimal and hence is an irrational number.

1. Visualise \(3.765\) on the number line, using successive magnification.

Solution:

\(3.765\) lies between the integers \(3\) and \(4.\) We divide the line segment between these integers into ten equal parts. Then, we note that \(3.765\) lies between \(3.76\) and \(3.77.\) Dividing the line segment between these two now into ten equal parts, we notice that the fifth part corresponds to the number \(3.765\) as shown in the image below:

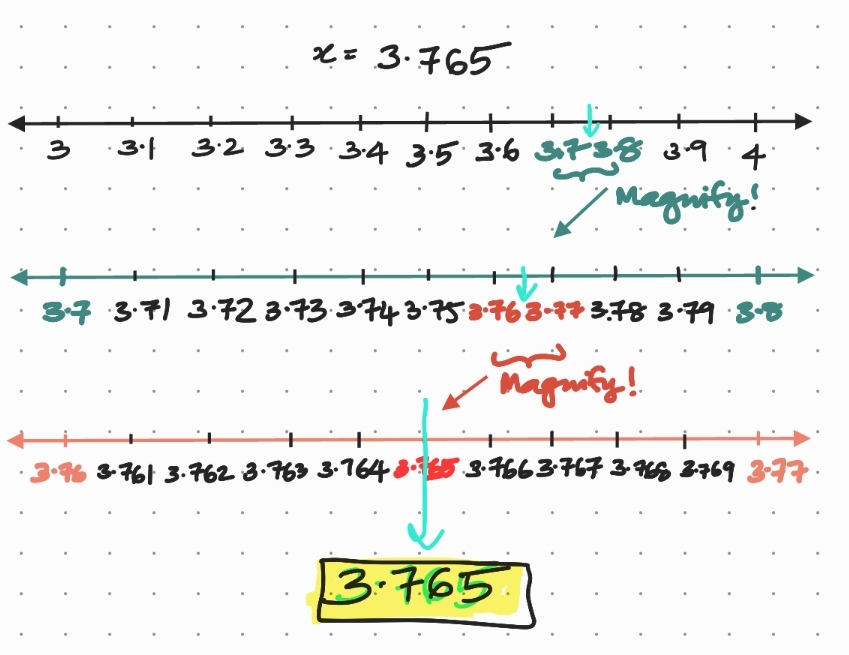
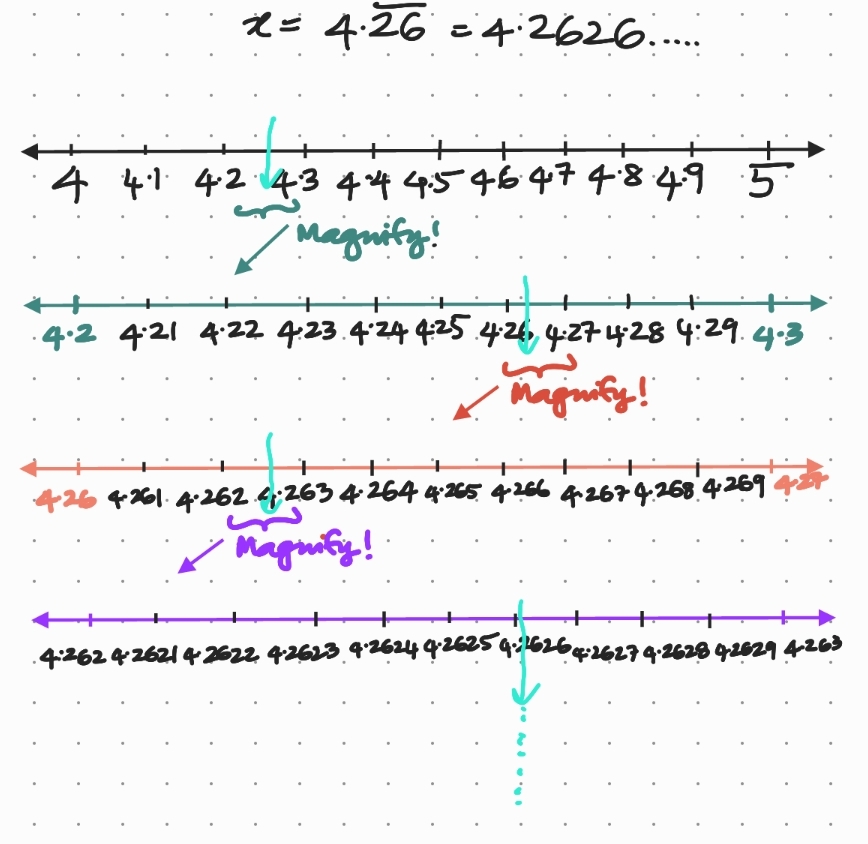
2. Visualise \(4.\overline{26}\) on the number line, up to \(4\) decimal places.

Solution:

We first note that \(4.262626…\) lies between \(4\) and \(5.\) We divide the line segment between these integers into ten equal parts. Now, \(x=4.\overline{26}\) lies between \(4.2\) and \(4.3.\) We divide this space into ten equal parts and note that \(x\) lies between \(4.26\) and \(4.27.\) Continuing this process two more times, we get the following visualisation of \(x\) upto \(4\) decimal places:

1. Classify the following numbers as rational or irrational:

(i) \(2-\sqrt5\) (ii) \((3+\sqrt{23})-\sqrt{23}\) (iii) \(\frac{2\sqrt7}{7\sqrt7}\) (iv) \(\frac{1}{\sqrt2}\) (v) \(2\pi\)

Solution:

(i) The difference of a rational number and an irrational number is irrational. Thus, \(2-\sqrt5\) is irrational.

(ii) \((3+\sqrt{23})-\sqrt{23}=3\) is an integer, and hence is a rational number.

(iii) \(\frac{2\sqrt7}{7\sqrt7}=\frac27\) is of the form \(\frac{p}{q}\) where \(p\) and \(q\) are integers and \(q\neq 0,\) and hence is a rational number.

(iv) \(\frac{1}{\sqrt2}\) is the quotient of a non-zero rational number and an irrational number, and hence is irrational.

(v) \(2\pi=2\times \pi\) is the product of a non-zero rational number and an irrational number, and hence is irrational.

2. Simplify each of the following expressions:

(i) \((3+\sqrt3)(2+\sqrt2)\) (ii) \((3+\sqrt3)(3-\sqrt3)\) (iii) \((\sqrt5+\sqrt2)^2\) (iv) \((\sqrt5-\sqrt2)(\sqrt5+\sqrt2)\)

Solution:

(i) \((3+\sqrt3)(2+\sqrt2)=3(2)+3(\sqrt2)+\sqrt3(2)+\sqrt3\sqrt2=6+3\sqrt2+2\sqrt3+\sqrt6\)

(ii) Since \(({\color{red}{a}}+{\color{blue}{b}})({\color{red}{a}}-{\color{blue}{b}})={\color{red}{a}}^2-{\color{blue}{b}}^2,\) we have:

\(({\color{red}{3}}+{\color{blue}{\sqrt3}})({\color{red}{3}}-{\color{blue}{\sqrt3}})={\color{red}{3}}^2-{(\color{blue}{\sqrt3})}^2=9-3=6\)

(iii) Since \(({\color{red}{a}}+{\color{blue}{b}})^2={\color{red}{a}}^2+2{\color{red}{a}}{\color{blue}{b}}+{\color{blue}{b}}^2,\) we have:

\(({\color{red}{\sqrt5}}+{\color{blue}{\sqrt2}})^2={(\color{red}{\sqrt5})}^2+2{\color{red}{\sqrt5}}{\color{blue}{\sqrt2}}+{(\color{blue}{\sqrt2})}^2=5+2\sqrt{2\times 5}+2=7+2\sqrt{10}\)

(iv) Using the identity \((a+b)(a-b)=a^2-b^2,\) we have:

\((\sqrt5-\sqrt2)(\sqrt5+\sqrt2)=(\sqrt5)^2-(\sqrt2)^2=5-2=3\)

3. Recall \(\pi\) is defined as the ratio of the circumference (say \(c\)) of a circle to its diameter (say \(d\)). That is, \(\pi =\frac{c}{d}.\) This seems to contradict the fact that \(\pi\) is irrational. How will you resolve this contradiction?

Solution:

Note that \(\pi\neq \frac{22}{7}.\)

In fact, \(\pi=\frac{c}{d}=3.1415926535…\) is an irrational number as its decimal expansion is non-terminating and non-repeating and \(\frac{22}{7}=3.142857142857…=3.\overline{142857}\) is a rational number as the decimal expansion is non-terminating and repeating.

\(\frac{22}{7}\) is just an approximation of \(\pi\) that helps make calculations easier. Thus, there is no contradiction!

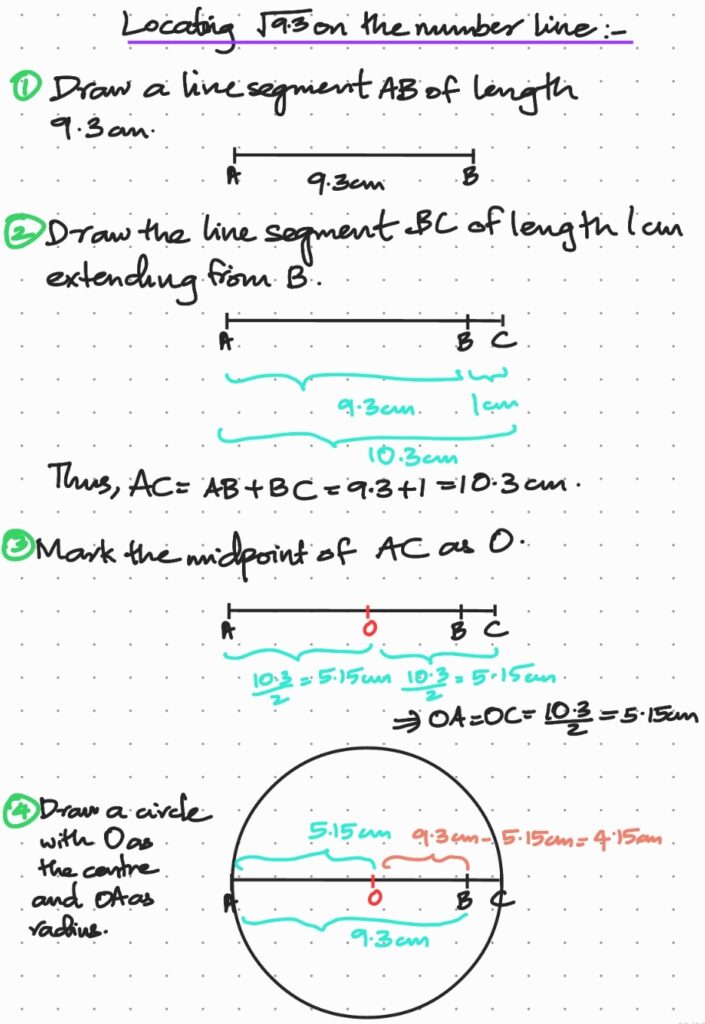
4. Represent \(\sqrt{9.3}\) on the number line.

Solution:

5. Rationalise the denominators of the following:

(i) \(\frac{1}{\sqrt7}\) (ii) \(\frac{1}{\sqrt7-\sqrt6}\) (iii) \(\frac{1}{\sqrt5+\sqrt2}\) (iv) \(\frac{1}{\sqrt7-2}\)

Solution:

(i) To rationalise the denominator of \(\frac{1}{\sqrt7},\) we multiply both the numerator and the denominator by \(\sqrt7.\)

\(\implies \frac{1}{\sqrt7}=\frac{1}{\sqrt7}\times \frac{\sqrt7}{\sqrt7}=\frac{1\times \sqrt7}{\sqrt7\times \sqrt7}=\frac{\sqrt7}{7}\)

(ii) To rationalise the denominator of \(\frac{1}{\sqrt7-\sqrt6},\) we multiply both the numerator and the denominator by \(\sqrt7+\sqrt6.\)

\(\implies \frac{1}{\sqrt7-\sqrt6}=\frac{1}{\sqrt7-\sqrt6}\times \frac{\sqrt7+\sqrt6}{\sqrt7+\sqrt6}=\frac{\sqrt7+\sqrt6}{(\sqrt7-\sqrt6)(\sqrt7+\sqrt6)}\)

Using the identity \((a+b)(a-b)=a^2-b^2,\) we have:

\(\frac{1}{\sqrt7-\sqrt6}=\frac{\sqrt7+\sqrt6}{(\sqrt7)^2-(\sqrt6)^2}=\frac{\sqrt7+\sqrt6}{7-6}=\sqrt7+\sqrt6\)

(iii) \(\frac{1}{\sqrt5+\sqrt2}=\frac{1}{\sqrt5+\sqrt2}\times \frac{\sqrt5-\sqrt2}{\sqrt5-\sqrt2}=\frac{\sqrt5-\sqrt2}{(\sqrt5)^-(\sqrt2)^2}=\frac{\sqrt5-\sqrt2}{5-2}=\frac{\sqrt5-\sqrt2}{3}\)

(iv) \(\frac{1}{\sqrt7-2}=\frac{1}{\sqrt7-2}\times \frac{\sqrt7+2}{\sqrt7+2}=\frac{\sqrt7+2}{(\sqrt7)^2-(2)^2}=\frac{\sqrt7+2}{7-4}=\frac{\sqrt7+2}{3}\)

1. Find:

(i) \((64)^{\frac12}\) (ii) \(32^{\frac15}\) (iii) \(125^{\frac13}\)

Solution:

(i) \((64)^{\frac12}=(8^2)^{\frac12}=8^{2\times \frac12}~ ~ ~ (\because (a^m)^n=a^{mn})\)

\(\therefore (64)^{\frac12}=8^{1}=8\)

(ii) \((32)^{\frac15}=(2^5)^{\frac15}=2^{5\times \frac15}~ ~ ~ (\because (a^m)^n=a^{mn})\)

\(\therefore 32^{\frac15}=2^{1}=2\)

(iii) \(125^{\frac13}=(5^3)^{\frac13}=5^{3\times \frac13}=5^1=5\)

2. Find:

(i) \(9^{\frac32}\) (ii) \(32^{\frac25}\) (iii) \(16^{\frac34}\) (iv) \(125^{-\frac13}\)

Solution:

(i) \(9^{\frac32}=(3^2)^{\frac32}=3^{2\times \frac32}~ ~ ~ (\because (a^m)^n=a^{mn})\)

\(\therefore 9^{\frac32}=3^{3}=27\)

(ii) \(32^{\frac25}=(2^5)^{\frac25}=2^{5\times \frac25}=2^{2}=4\)

(iii) \(16^{\frac34}=(2^4)^{\frac34}=2^{4\times \frac34}=2^3=8\)

(iv) \(125^{-\frac13}=\frac{1}{125^{\frac13}}~ ~ ~ (\because a^{-\frac{1}{n}}=\frac{1}{a^n})\)

\(\therefore 125^{-\frac13}=\frac{1}{(5^3)^{\frac13}}=\frac{1}{5^{3\times \frac13}}~ ~ ~ (\because (a^m)^n=a^{mn})\)

\(\therefore 125^{-\frac13}=\frac{1}{5^1}=\frac15\)

3. Simplify:

(i) \(2^{\frac23}\times 2^{\frac15}\) (ii) \((\frac{1}{3^3})^7\) (iii) \(\frac{(11)^{\frac12}}{(11)^{\frac14}}\) (iv) \(7^{\frac12}\times8^{\frac12}\)

Solution:

(i) \(2^{\frac23}\times 2^{\frac15}=2^{\frac23+\frac15}~ ~ ~ (\because a^m\times a^n=a^{m+n})\)

\(\therefore 2^{\frac23}\times 2^{\frac15}=2^{\frac{10+3}{15}}=2^{\frac{13}{15}}\)

(ii) \((\frac{1}{3^3})^7=\frac{1^7}{(3^3)^7}~ ~ ~ (\because (\frac{a}{b})^m=\frac{a^m}{b^m})\)

\(\therefore (\frac{1}{3^3})^7=\frac{1}{3^{3\times 7}}~ ~ ~ (\because (a^m)^n=a^{mn})\)

\(\therefore (\frac{1}{3^3})^7=\frac{1}{3^{21}}=3^{-21}~ ~ ~ (\because \frac{1}{a^n}=a^{-n})\)

(iii) \(\frac{11^{\frac12}}{11^{\frac14}}=11^{\frac12-\frac14}~ ~ ~ (\because \frac{a^m}{a^n}=a^{m-n})\)

\(\therefore \frac{11^{\frac12}}{11^{\frac14}}=11^{\frac14}\)

(iv) \(7^{\frac12}\times8^{\frac12}=(7\times 8)^{\frac12}~ ~ ~ (a^m\times b^m=(ab)^m)\)

\(\therefore 7^{\frac12}\times8^{\frac12}=56^{\frac12}\)